Practical computation of error and uncertainty using traditional methods is hampered by many difficulties. For example, the ‘Differential method’ using partial differentiation requires ‘small errors’ and the functions must be simple with a low number of variables. In academics, effective instruction of error analysis during freshman-level science laboratory courses is prevented because multi-variable calculus is typically not covered until the sophomore year. These practical and academic problems pose the main motivations for a mathematics project to pursue new error analysis methods. The goals are to obtain speedier and more robust methods, make them accessible to students and be suitable for practical applications in a wide range of fields from science, engineering, medicine to finance. The impact is potentially anywhere numbers are used to measure, indicate and calculate.
This mathematical project started with the recognition of the geometric nature of quantifying a single physical event and the error that accompanies all numbers that quantify things such as money, interest rates, temperature, blood pressure and wind speed. This is a hybrid representation incorporating numbers as scalars for geometric elements. Consequently, traditional number arithmetic, such as addition, subtraction, multiplication and division must be replaced by geometric arithmetic that respects both the number and geometric aspects. The geometric arithmetic must also handle mathematical functions used in science, finance and other fields. This includes statistical, trigonometric, exponential, logarithm and hyperbolic functions found both on handheld calculators or built into software packages. The effort expended on the mathematics is successful if it enhances understanding and is a solid basis for writing software for computers and handheld devices. Its generic nature makes the mathematical gains applicable to all practical applications.
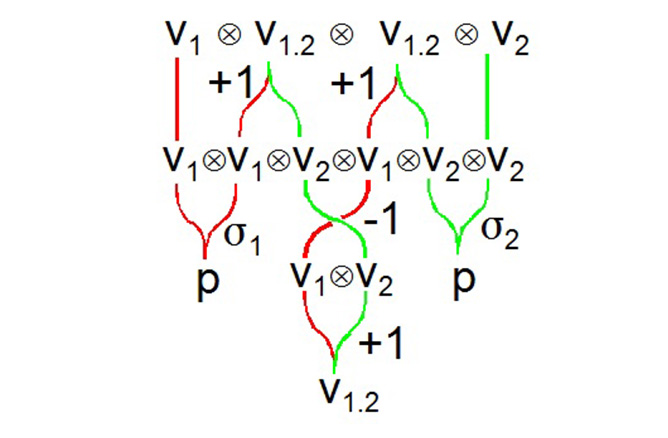
A survey of accomplishments for the mathematical project includes identification of initial point and line varieties, establishment of addition and multiplication quasigroups for points, vectors, chordals and duals, and derivation of axioms from geometric principles. These landmarks were followed by power-of-dual theorem, function-of-dual theorem and posing trans-imaginary numbers for implementation of duals arithmetic. For example, the braid diagram shown gives an example of multiplication of vector-based geometry along with the point geometry acting as an identity. Practical results obtained included the coding and testing of the CertainError geometric arithmetic with software such as EXCEL, MATLAB and LabVIEW. Another practical result is the coding of a CertainError APP for error propagation calculations on the iPhone and Android platforms that is intended to replace typical scientific calculators.
Numerous examples have demonstrated the effectiveness of this mathematical project for both understanding and practical results. Advantages over known methods such as Monte-Carlo, Differential and Interval have also been demonstrated with examples such as the Black-Scholes Formula in the Finance field. Highlights of this ‘competition’ have been the superiority of the duals arithmetic to solve the dependency problem (see spreadsheet below) and navigate divide-by-zero-with-error and square-root-of-negative calculation faults. The computational speed and informational advantages of duals arithmetic have also been demonstrated.