READ FULL REPORT:
Uncertainty Arithmetics Applied to the Black-Scholes Model by Ronald LaFleur.pdf
BACKGROUND:
In ‘long selling’ the buyer of shares of stock presumably wants the shares because they expect an increase in value over the time and expect to sell it to someone else in the future. But what if you expect the value of the shares to decrease? You can make money if this happens if you ‘short sell’ the shares. That is, you sell shares you do not own but have borrowed and agree to buy the shares back (repurchase) in the future, giving the shares back to the lender to make things square. It is like someone ordering a pair of shoes from you. You are selling a pair of shoes to them at today’s price and you agree to deliver the actual shoes in a week’s time. During that week you find a supplier that has the shoes at a cheaper price and you buy them. The cheaper, the better. At the end of the week you ship the shoes to the person that ordered them and make a profit. So here, you can make a profit by selling something you do not actually own. From the examples of long and short selling, we see that share ownership is a bit intangible depending on the timing of buying and selling.
Another level above short selling is the ‘option’ (noun). That is you do not buy and sell the shares but instead buy or sell the option to buy or sell the shares. The option can be structured different ways to manipulate the timing and represent your expectations of the future price. The option ‘derives’ its value from the underlying shares and that is why it is called a ‘derivative’ (sorry to disappoint the fans of calculus). There are many aspects of the option that have to be structured but in the end, the option to buy or the option to sell the share may not be exercised and the option has an expiration date. If so, you can walk away from the option, possibly losing only the initial fees.
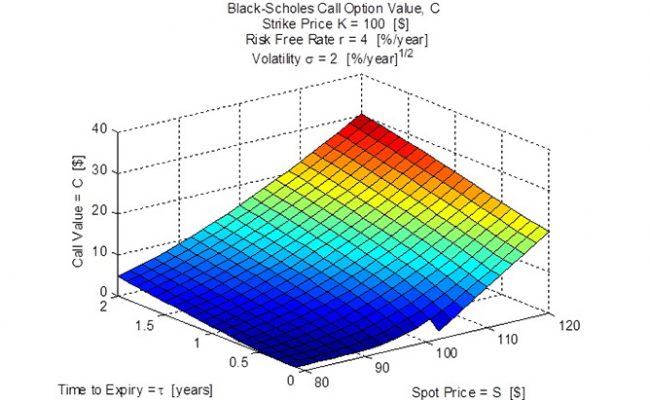
To make decisions when the option is structured, a calculation is performed to project the future value of the underlying share and discount it to today using an expected rate of growth. So if you expect a rate of growth over 10% over the option’s time and the future price is $110 per share, then it is discounted to $100 in today’s cost and this number is used when structuring the option. This calculation can also account for the volatility of the underlying share as the growth rate will probably vary up or down over the time of the option. The Black-Scholes Option Formula provides a basis to calculate options and has the built-in features of mean growth rate, volatility (rate fluctuation), probability for growth and probability for decline. Published in 1973, the article ‘The Pricing of Options and Corporate Liabilities,’ led to the award of a Nobel Prize in Economics in 1997. Despite mixed reviews in practice, the Black-Scholes Option Formula remains a topic of interest. For typical use, five numbers input to the Black-Scholes Option Formula are the time-to-expiry, risk-free rate, strike price, spot price and volatility with the calculation of the option value. Each of these can be set to base values or varied over a grid and uncertainty can be included to represent a spread of possible values that could occur over the life of the option.
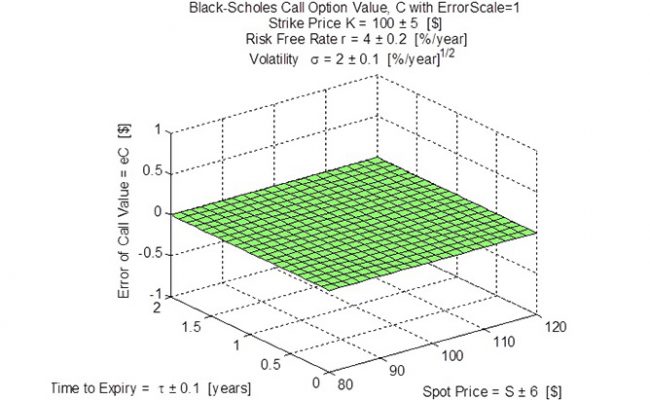
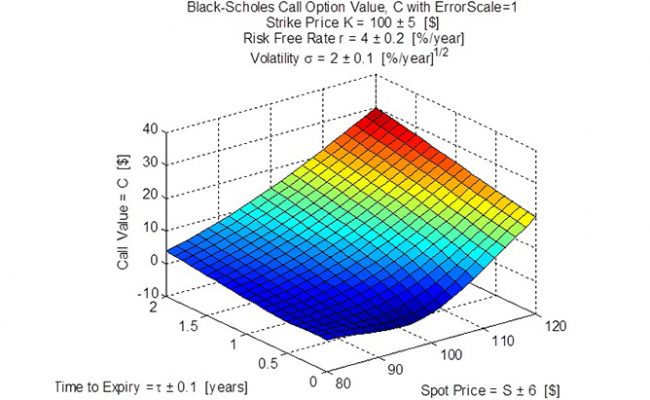
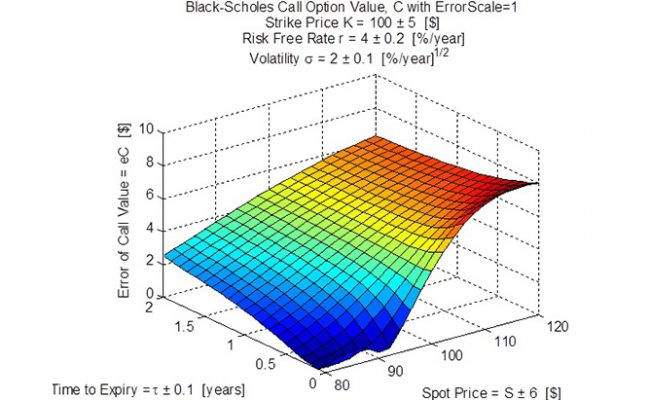
The Black-Scholes Option Formula project was initiated to demonstrate different uncertainty arithmetics and provide an ‘example of substance’ familiar to people in finance. The project started with the formatting of the formula into a series of 21 calculation steps, five of which involve the input numbers and their uncertainty. The 21 step procedure involved operations of square root, multiplication, exponentiation, division, natural logarithm, addition, subtraction and the cumulative normal distribution. As verification of the 21 steps, example numbers were calculated and compared to published call option response surfaces. After successful verification, the relevant steps of the calculation were converted to different uncertainty arithmetics, including duals arithmetic. For traditional arithmetic, Figure 1 (left-most image dot) shows the Call Value and Figure 2 shows the Error of the Call Value. For Duals arithmetic, Figure 3 shows the Call Value and Figure 4 (right-most image dot) shows the Error of the Call Value. It is important to note that the traditional arithmetic fails at very low time-to-expiry due to a divide-by-zero fault (there is a chunk of the surface missing on Figure 1). The error surface for traditional, Figure 2, is perfectly zero because uncertainty is not calculated with traditional arithmetic. The duals arithmetic is shown to be robust and can calculate all the way down to zero time-to-expiry (Figure 3). The error of call value surface, Figure 4, shows where lower error (uncertainty) can be obtained but this tends to correspond to low call value, so there is a trade-off between risk and reward.