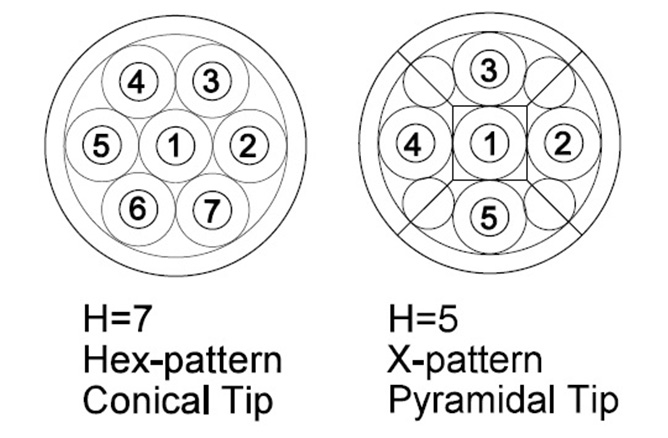
Aerodynamic testing of swirling flows, such as the flow exiting a turbine blade (gas or wind), requires the measurement of three components of velocity and static pressure. These four quantities can be extracted from a pressure probe with at least four distinct ports or holes. To do this, the probe has to be calibrated in a flow with known speed while pitch and yaw angle of the probe is adjusted to known values. This gives the pressure response of each port versus pitch and yaw angle. A calibration theory generates a calculation of four pressure coefficients that are independent of flow speeds below 20% the speed of sound. This allows the probe to be calibrated at one speed but then used to measure unknown flows at any speed.
Multi-hole probe calibration methods are distinguished by the definitions of the four pressure coefficients. Error propagates from the measured calibration pressures to the pressure coefficients and then continues from the four measured port pressures to the calculated components of velocity and static pressure. Then the error propagation is different for each method and it is possible to compare the different methods according to the resulting errors for the measured flow. The best method is the one that has the lowest velocity and pressure errors. Posing the pressure coefficients as ratios of general linear functions of pressure, the method with minimum error can be found. However, this idea is plagued with a divide-by-zero fault as the method parameter array becomes ‘perpendicular’ to the pressure array. There had been no solution to this problem and the optimization project was shelved for a few years. Eventually the duals arithmetic was developed and an inadvertent solution was found.
The duals arithmetic was found to be flexible (solves the dependency problem) and robust (capable of divide-by-zero-with-error). Thus the duals arithmetic offers the solution to the divide-by-zero fault when measurements are formatted along with their errors. The duals arithmetic has been applied to a five-hole probe. For example, the error for a flow measurement utilizes a 2D calibration panel (triangle interpolation of yaw and pitch angle) that amounts to a 33-dimensional error vector. This was used to successfully navigate the divide-by-zero fault and find methods with the least error localized to each triangular panel of the calibration. This offers a method for other kinds of multi-hole probes.